Calculate Percentage

Here are instructions for the formulas to calculate common percent related math problems:

• percentage
  • formula: (x/y) * 100 = z%
  • in words: divide x by y to get its decimal number & then multiply by 100 to convert the decimal into a percent
• number associated with a percentage
  • formula z% / 100 * x = y
  • in words: divide the desired resultant percent by 100 to convert it to a decimal, then multiply it by the original number to solve for the number which is associated with that percent of the original number
• percent change
  • formula: (y-x)*100/x = z% change
  • in words: subtract the original number from the final number, multiply this result by 100 (move the decimal 2 places to the right) and then divide this value by the original number to get percent change

A Practical Guide to Pervasive Percentages

We might not notice it, but percentages are quite common in daily life. Even if your work does not involve a lot of computing or mathematical concepts, you’re bound to encounter it now and then. For instance, when you check your mobile phone, its battery life is expressed in percent. A retail store is offering up to 50% off on jeans till the end of the month. When you catch the news, the weather anchor says there’s 30% chance of rain in your area.

In its most literal form, percentages mean “part per hundred.” This is the expression of a fraction or ratio where the denominator is 100. The percentage became one of the most popular expressions of fractions for a reason. They illustrate proportion and completeness in a way that’s easy to understand. They also simplify the process of calculating based on a proportion. Percentages convert to decimals, which are much easier to process.

Its usefulness in everyday arithmetic is evident wherever you look. We see percentages everywhere. You can find them in banks and stores to video game inventories. They all mean something different in context, yet use the same expression. Grasping basic percentages is a vital skill that can help you save time and money. Besides convenience, this is especially true when it comes to expensive purchases and investments.

The Fundamentals of Percentages

Much like fractions, percentages represent parts of a whole. All percentages are numbers divided by 100. A single percentage point, 1%, is equal to the fraction 1/100. Thus, you can convert them into ratios, decimals, or other fractions. Likewise, you can express any fraction, decimal, or ratio as a percentage.

You have several ways of converting a fraction into a percentage. The easiest percentage conversion is through decimals. Divide the fraction to get its decimal value, then multiply it by 100.

(x/y) * 100 = z%

Where:
x is the numerator
y is the denominator 
z is the percentage

For our first example, let’s find the percentage value of 6/8:

= (6 / 8) x 100%
= (0.75) x 100%
= 75%

When you already have the decimal value, move the decimal point two places to the left. Thus, 2% is 0.02 and 50% is 0.5.

Converting a percentage to a fraction or ratio is more complex. First, you must find the greatest common factor between the two numbers. Then you divide both the numerator and denominator by them. For instance, to simplify 5%, start by expressing it as 5/100. Then, divide the two numbers by their common factor, 5.

= (5 / 5) / (100 / 5)
= 1/20

To convert to a ratio, change the slash into a colon.

= 1:20

Remember that your denominator is always 100, and not all numbers will share its factors. Often, you can simplify many percentages by leaving them as is. For instance, 37% will be 37/100 because the common factor between the two numbers is 1.

Here’s how we can turn 37.5% into a decimal, fraction, and ratio:

= 37.5% / 100
= 0.375

The fraction form of 0.375 is 375/1000. Let’s simplify this fraction. The common factor of the two numbers is 5. With this in mind, how simple can this fraction go?

= (375 / 5) / (1000 / 5)
= 75/200
= (75 / 5) / (200 / 5)
= 15/40
= (15 / 5) / (40 / 5)
= 3/8 
= 3:8

The Limits of Base 100

As a number, 100 is very convenient compared with varying fractions. You can divide evenly it by 1, 2, 4, 5, and 10, which are easy numbers to remember. But notice that it isn’t divisible by 3, 6, 7, and 9. Once you convert them, you encounter the awkwardness of repeating decimals. Rounded off to 4 decimal places, 100/3 is 33.3333(…).

To display these as exact values, you must express them as fractions. You can, of course, get an approximate answer by rounding it off. In most practical cases, it’s not an issue. Of course, you don’t need to fret at all if you deal with 99.9999(…)%. In the most familiar model of arithmetic, you can go ahead and say it’s 100%.

Both percentages and fractions are ways to describe ratio. Ratio can be defined as the numerical relation between two figures which shows the number of times one value is contained within the other. To help you visualize it better, imagine a whole box broken into 100 equal parts, where each part is equivalent to a single percent.

The following box represents the whole. It has 100 small boxes:

• Each small box is equal to 1% of the whole. The red box is 1%.
• Two boxes are equal to 2%. This represents the blue boxes.
• Five boxes are equal to 5%. This represents the green boxes.
• Twenty-five boxes are equal to 25%, which is 1/4 of the entire box. This represents the gray boxes.
• Fifty boxes are equal to 50%, which is 1/2 of the whole. This represents the yellow boxes.

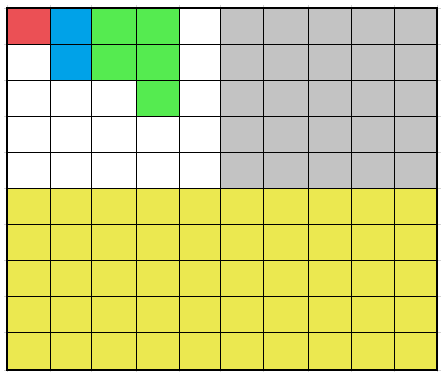
Out of 100 colored boxes, 17 are white and 83 are colored. Thus, we can say that 17% of the box is white, while 83% of the box is colored.

Why do we use percentages? This concept makes calculating simpler when we’re working with parts of 100. Again, it’s easier than basing calculations on thirds, fifths, twelfths or other bases. It’s useful in particular because many fractions do not have a precise non-recurring decimal equivalent.

Thinking in terms of percentages also makes it easier to compare the amount of figures between each other. With a common denominator of 100, you’ll get a clearer idea of how much more or less a figure represents compared to another.

Applying Basic Percentage Calculations

For example, a classroom has 40 students. If we say 25% of the class are girls, you’ll get the idea that most of the students are boys (75%). That means out of 40 students, there are only 10 girls while there are 30 boys.

While it’s easy when you’re working with a figure that’s exactly 100, what about other numbers? In the example, the whole number is 40. We know that 50% or half of 40 is 20, and 25% or ¼ of 40 is 10. But how do we calculate this? Here’s the basic percent formula you can use:

(x/y) * 100 = z%

Where:
x = the part of the whole (numerator)
y = the whole number (denominator)
z = the percentage

*After dividing the part with the whole number, the figure is multiplied by 100 to convert the decimal number into its percentage form.

To easily compute percentage problems, use the above calculator on our page.

Let’s say a classroom has 40 students. 30 students are boys, while 10 students are girls. What % of the class are girls, and what % of the class are boys? Refer to the solution below.

Solving for the % of girls	Solving for the % of boys
x = 10 girls	x = 30 boys
y = total number of students, 40	y = total number of students, 40
= (10/40) x 100	= (30/40) x 100
= 0.25 x 100	= 0.75 x 100
= 25%	= 75%
Out of 40 students, 25% are girls.	Out of 40 students, 75% are boys.

Now, let’s say a class of 40 students had 25% girls and 75% boys. Then you’re asked to determine the precise number of boys and girls in the class. How do you do this? Simply change the formula a bit to solve for x:

(z% / 100) * y = x

Solving the number of girls	Solving for the number of boys
y = total number of students, 40	y = total number of students, 40
z = 25% are girls	z = 75% are boys
= (25% / 100) x 40	= (75% / 100) x 40
= 0.25 x 40	= 0.75 x 40
= 10	= 30
Out of 40 students, 10 are girls.	Out of 40 students, 30 are boys.

At this point, you might be wondering if there is any relevance to knowing the ratio between boys and girls. Or if the ratio of anything is important at all. In reality, you encounter percentages a lot whenever you shop. Gone grocery shopping or bought anything lately? When you see discounts and markdowns, you immediately know you can purchase a product for a lower price. That % is based on the original price, which is the whole amount you would have paid if it weren’t for the discount. Nowhere is % more apparent when it comes to buying and finances. We’ll talk about this more in the latter sections of our article. 

A History of Percentages

The system of using percentages came long before the idea of decimals. People have used fractions to calculate taxation and tithes for millennia. It was the Ancient Romans, however, who popularized the use of fractions based on 100. The word itself comes from the phrase per centum. This means “by 100” in Latin, the Roman language.

During the reign of the Emperor Augustus (23 BCE – 14 CE), the Imperial government began to charge a tax on auctions. Called centesima rerum venalium, it cost 100th of the value of the goods sold. This tax helped pay for the retirement stipends of the Roman legionary army.

Long after Roman power faded in Europe, their influence remained strong. Educated people still used Roman numerals and divided things based on 100. By the Renaissance, wealthy merchants dealt with greater sums of money. Dividing by 100 simplified the need to keep track of their cash.

We can still see this today in the way we divide money. At present, most currencies are in decimals. Subdivisions of the U.S. dollar, for instance, are called cents, after the Latin word for 100. A single penny is one cent, or 1/100th of a dollar.

Did You Know?

When it comes to word usage, in American English, % is often written as one word, “percent.” However, in British English, % is commonly written as two words, which is “per cent.” But even in the British usage, the words percentage and percentile are written as one word.

The Percent Sign

It is forgivable to assume that the percentage sign "%" depicts a fraction. It does look like one at first glance, as does the division symbol, the obelus (÷). You may also question why the symbol has two zeroes in it. After all, isn’t dividing by zero undefined? Some sources claim that the two circles represent a shorthand for one hundred. That, while sort-of true, is not the whole story. The story behind it is much more complex.

Much like the ampersand (&), the percentage sign began as a shorthand of a phrase. The symbol was unknown before 1425. Back then, people in Europe expressed percentages in an abbreviation called pc^o. This is the shorthand for the phrase per cento, the Italian version of the original Latin phrase.

Other writers sometimes added a line under the p (ꝑ) to show its use as an abbreviation. By the 1600s, the shorthand evolved into a glyph; the c turned into a circle, which rested on top of a line. The o became the bottom circle. Over time, writers began using just the glyph, which resembled an obelus. Incidentally, it was around the same time when the obelus was used as a symbol for division. 

The two circles, together with the line, represent the number 100. By the 1800s, the modern percent symbol dropped the p abbreviation that preceded it. Writers also slanted the line between the two circles.

The Permille and Permyriad

Its resemblance to a fraction didn’t go unnoticed, though. Soon, the percentage sign led to a set of symbols representing multiples of 10. One symbol, the permille sign (‰), emerged to depict parts per thousand. Meanwhile, the permyriad (‱) measures parts per ten thousand.

Both are found in specific circumstances. Scientists use permilles in measuring trace amounts in solutions. The concentrations in these cases are very low. Permyriads, meanwhile, find use in the realm of finance. Financial professionals use them to measure basis points, which are far lower than percentage points.

Percentages as a Measurement

Comparing portion sizes is one key to the popularity of percentages. People find it easier to compare percentages than fractions. This is the reason why third pound burgers never quite took off in the United States. The target audience didn’t realize that these were heavier than quarter pound burgers. Thus, even marketing departments often use percentages over fractions to tout larger sizes.

People use percentages to compare things in three different ways:

• Measuring changes in size: Percentages measure how much a thing changed in size or value relative to how it was before. For instance, an investor’s portfolio may have grown in size by 4% of its original value over the past year.
• Measuring differences in rates: You can measure the difference between rates from two periods via percentage points. Experts use the changes in growth rates to measure national economic performance. If the growth recorded is positive, it indicates rising growth.
• Measuring differences in proportion: Percentages distinguish between population subsets and measure their size relative to the whole. Market researchers, for instance, use these to determine brand popularity. They can, for example, say that a brand of soap is the most popular if at least 51% of the population prefer it.

Each of these comparisons derive the percentage in different ways. When measuring changes in size, you compare the difference between the new value and the old one. In our first example, let’s assume that the investor’s starting principal is $2,000. If the growth is 4%, here’s how much they made over the year.

= $2,000 x 4%
= $2,000 x 0.04
= $80

Finding the difference in rates is more complex. In our second example, let’s assume that the country’s gross national product grew by 2%. This year, it grew by 2.5%, a change of 0.5 percentage points. This number seems unimpressive at first glance, but is it? Thus, we must look below the surface. How much did the percentages change? Let’s find the percentage change through the following formula:

[(y – x) * 100] / x = z%

Where:
y is the present value
x is the previous value
z is the percent change of these values

= [(2.5 – 2) * 100%] / 2
= [0.5 * 100%] / 2
= 50% / 2
= 25%

Analyzing changes in percentages puts things in perspective. While this year’s GDP grew 0.5% higher than last year, it represents a 25% change in growth rates over that period. And because economies are large, even these tiny changes can spell good (or bad) news for everyone. 

Before you begin, find out the total number of people in the population set or sample. Next, you record the number of each of the responses within the set. In our third example, the product survey, we’ll assume the following details:

• A population size of 5,000 respondents
• Three different soap brands (brands X, Y, and Z)

Here’s the tally of the number of responses for that survey:

Brand Preference	Number of Respondents	Percentage
Brand X	3,026	60.52%
Brand Y	1,278	25.56%
Brand Z	541	10.82%
No Brand Preference	155	3.1%

Taken together, those who prefer other brands or no brands in particular comprise 39.48% of the sample. In most cases, the total percentage will tally to exactly 100%. In some statistical situations, the percentages may fall short or exceed 100%. When the tally falls short, this is often because of rounding. Overshooting, meanwhile, is often the result of people identifying with more than one option.

Rates

A rate is a ratio that compares two distinct units. In its most common form, it is a charge based on another amount. Fuel efficiency rates, for instance, measure the distance your vehicle can travel for every unit of fuel it consumes. If a car reaches 50 miles per gallon, it is far more efficient than a car that goes 25 miles per gallon. This becomes essential when calculating how much you spend on fuel with each trip.

In finance, economics, and statistics, rates are expressed as percentages. These state the amount of growth over a specific period. Interest rates, for instance, refer to the fee you must pay each year for the amount of money you borrowed.

Bigger than a Hundred

In everyday speech, people mention percentages greater than 100 as a convenient hyperbole. When you give 150%, it indicates a level of dedication far beyond what’s needed. People do use percentages above 100 in a literal context.

Often, they involve measuring exponential growth or size differences. A 50% growth rate, for instance, indicates that something grows by half its size or value. A rate of 200% shows growth that’s twice the original value, and so on.

When you do find percentages expressed in the hundreds, it will sound alarmist. It likely is for a good reason. Anything that grows twice its size in a short span is worth paying attention to. If, for instance, your sales grew by 400% last year, you must re-examine how you did it. Meanwhile, if your debts grew by 400%, you must re-evaluate your financial strategy.

Common Percentage Mistakes

We tend to misunderstand percentages, especially for something we use all the time. Fortunately, we can avoid some of the most egregious missteps. A good way to avoid mistakes is to clarify how we use percentages in a given context.

One common error is when interpreting percentages is when measuring growth. For instance, let’s assume you and your company sold 10,000 bags of cake flour in 2019. In 2020, that number increased by 60,000 bags. It’s tempting to say that your sales grew by 600%.

Sure enough, your total sales in 2020 are 600% of your sales the year before. But that’s not how much your sales grew. To measure growth, start instead with a base amount and subtract it from the present amount. Our base amount is the volume of sales in 2019. Here’s how much your sales have changed.

= (60,000 – 10,000) / 10,000
= 50,000 / 10,000
= 500%

While you sold 600% more units, your annual growth was 500%. This represents the sales above those needed to match the previous year’s numbers. Bear your starting and ending points in mind when calculating percentage growth.

Another common mistake is interpreting differences in percentages. Sometimes, readers jump to conclusions without looking at the percentages up close. We’re tempted to think that a greater value indicates a greater percentage growth. But that’s not always the case. For instance, suppose that the price of a video game went up from $15 to $30 one year. The following year, it increased to $50.

On the surface, it’s easy to think that the second year had a higher percentage of growth. After all, the price increase of the second year (20) is bigger than the first’s (15). But think again. In the first year, the price grew by 100%.

= (15/15) x 100%
= 1 x 100%
= 100%

The following year, the price grew only by 66.67% or a third.

= 20/30 x 100%
= 0.6667 x 100%
= 66.67%

You may also encounter ambiguity expressing percentage changes in a sentence. We can see this in action when discussing interest rates. Let’s assume the present interest rate was 2%. If the rate increased by 5%, what does this mean? Most laypeople will assume that it means it increased to 7%. However, it can also mean that it increased by 5% of 2%. This leads to the total of 2.01%, which is a lot less impressive.

Whenever possible, use clear terms to avoid ambiguity. In our example, it’s better to say that the rate changed by 5 percentage points, rather than by 5%. 

Remember: Percentages never cancel out.

Here’s another common example. Let’s say you increased a number by 30%, then reduced it by another 30%. You might expect to end up with the same number you started with. But you don’t. This assumption is incorrect.

Given how we base percentages on a 100 denominator, it’s understandable why this is confusing. We tend to presume we are starting with the same whole number. When in reality, increasing or decreasing that number has changed the basis for the percentage.

For a simpler example, say you have 100 objects and decreased that by 30%. You are left with 70 objects.

= 100 – 30%
= 70

Now, if you increase 70 by 30%, you get 91. Notice that it does not restore the number of your objects to 100. This is because 30% of 70 is equal to 21.

= 70 + 30%
= 91

In the first part, we took 30% of 100. In the second part, we took 30% of 70. Again, the basis for the percentage changes each time you increase or decrease its value. Take note of this to avoid making the same mistake.

Working with Populations

Percentages are an important component of analyzing statistical data. These let you show the differences in the subsets of a population with relative ease. They also serve as a template for visual aids. You can use the fraction method above to find the percentage of a subset relative to the population size.

Working backwards, you can find the value a percentage as long as you know the size of the population. To find the numerical value of the percentage, use this formula:

z% / 100 * x = y

Where:
x is the population or sample
y is the subset
z is the percentage

Let’s see this in action. Suppose you’ve read an article on the local news that says 12% of respondents prefer pineapple on a pizza. Most news articles will not provide the tabular data of surveys like this. They might, however, mention the population size of that survey. In our example, the article mentions that the surveyors interviewed 5,000 people. Without looking at the study’s data, we can determine how many people gave that answer:

= (12% / 100% ) x  5,000
= 0.12 x 5,000
= 600

To make an accurate assessment, we must know the size of the sample the percentage comes from. Can the sample represent the population at large? Only if it’s big enough. For instance, brands love touting that “9 out of 10 people” recommend them. If they only had a sample size of 10 people, that’s not definitive.

Quantity Comparison

Proportions matter when you’re making chemical formulations. To achieve the desired results, you must use the appropriate proportions of ingredients. To create a bigger batch, you must double the ingredients according to their proportion. Knowing these percentages will help you create a consistent product.

This becomes especially important when dealing with active ingredients. During COVID-19 pandemic, for instance, hand sanitizer has become hard to find. So, a lot of people began searching for ways to make it themselves. According to the Centers for Diseases Control and Prevention (CDC), hand sanitizer must comprise at least 60% alcohol to be effective. If you start off with a 99 percent alcohol solution, you can use 2/3rds of it in a mixture. The resulting hand sanitizer will be 66 percent alcohol, well within CDC parameters. If you start with a 70% commercial alcohol solution, however, the resulting mixture will be much too low.

You also need exact measurements when you’re baking. To get the desired texture and consistency, you must make sure you only use the amounts you need. It can be hard to determine precise measurements for non-fluid ingredients. Thus, bakers have a specific system to measure percentages based on the weight of the ingredients.

Sales Tax, Discounts, & Coupons

Percentages first came into widespread use to make calculating taxes easier. Even today, the government measures taxes in percentages. In many places, there’s a value-added tax on retail items. In some places, retailers do not add sales taxes into the final price. Thus, it can be a rude surprise when you get to a checkout. This can make it rather difficult to stay on a budget.

Using percentages, you can derive the extra you might add to the price. Learn the rates of your local and state taxes and apply them each time you buy.

Retailers jostle for your attention by marking down their prices using percentage discounts. On the surface, they can be very tempting. How good a deal they are depends on the size of the discount. A price cut that’s 20% off is good, depending on the item you’re buying. A 50% discount, when you can find one, is even better.

Even when you’re not on a budget, don’t forget to calculate discounts and coupons when you’re shopping. Whether you’re buying an expensive gadget, a simple item, or groceries, it’s still better to save several bucks (or even a hundred) than none at all.

Let’s suppose you’re looking for a new pair of running shoes. Luckily, the apparel store put 30% off on their shoes. And you, being a wise shopper, also saved a coupon for 15% off on any item. The store allows you to use the coupon even if the shoes already have a discount. If the running shoes you want costs $80, how much would it cost with the discount and coupon?

If you’re not used to calculating in percentages, you might think 30% and 15% off would mean 45% off. This is wrong. Percentages do not work that way. What you do is take 30% off and compute it with the original price. Then, you take 15% off from the coupon and also compute it with the original price.

First, ask what is 30% of $80? Convert the percentage to decimal and solve it like this:

= 0.30 x $80
= $24

Now you know $24 is the discount amount. We then subtract this amount from the original price.

= $80 – $24
= $56

With 30% off, the sale price for the running shoes is $56. Now, let’s solve the 15% off coupon discount.

= 0.15 x $80
= $12
= $56 – $12
= $44

Since the running shoes’ sale price is $56, we’ll subtract $12 from this amount. From an original price of $80, because of the discount and coupon, the running shoes are now only $44. But hold on right there. Most states in the U.S. impose sales tax, and this applies to retail purchases. As of this writing, only five states currently do not enforce sales tax: Oregon, Montana, Delaware, New Hampshire, and Alaska.

Using our previous example, let’s suppose the sales tax on retail is 9%. To calculate this, the tax is based on the item’s sale price. So we should ask, how much is 9% of $44?

= 0.09 x $44
= $3.96

$3.96 is the sales tax. Now, we add this tax to the sales price.

= $44 + $3.96
= $47.96

From an original price of $80, the running shoes now cost $47.96. After discounts and the sales tax, you actually save $32.04 on your purchase.

Giving Tips at Restaurants

It’s important to know how much tip you’ll give in a restaurant. This way, you’re not giving too much or too little to your waiter. Depending on where you’re dining, make sure to research the average tipping rate. According to Consumer Reports, for starters, a basic rule in restaurant tipping is to leave between 15% to 20% of your total pre-tax restaurant bill. Never leave below 15% unless you believe the service was really bad. If your server was rude or offensive, speak to the manager. This feedback will help improve the establishment’s customer service.

For example, you dined out with two friends and split the bill equally. Your total bill was $89.50 and you intend to give a 20% tip. You can calculate the tip before or after you split the bill. Since it’s a real-life scenario, it’s acceptable to round the total bill to $90. Its easier to split it in thirds this way.

Split the Bill Before Computing the Tip	Compute the Tip Before Splitting the Bill
$90 / 3 = $30 each	20% of $90 is $18.
Now find 20% of $30 and add that as the tip.	The total bill amounts to:
20% of $30 is $6.	$90 + $18 = $108
Now, add that $6 to $30. This amounts to $36.	Now, split the total bill in thirds: $108 / 3 = $36
Total share: Each of you would pay $36.	Total share: Each of you would pay $36.

Federal Income Tax Rates

Percentages matter when tax season rolls in. This is where things can get complex. For instance, the U.S. Federal government charges a progressive tax rate on incomes. The government divides income tax rates based on brackets. People with higher incomes owe higher taxes.

Those who fall on a higher tax bracket don’t need to pay the higher rate on all their income, though. They first must pay the lower rate for the part of their income that falls under the first bracket. Then, they pay the higher rate on the remaining income.

For example, in 2021, U.S. Federal marginal tax rates are as follows:

Tax Rate	Single	Head of Household	Married Filing Jointly / Qualified Widow(er)	Married Filing Separately
10%	$0 – $9,950	$0 – $14,200	$0 – $19,900	$0 – $9,950
12%	$9,951 – $40,525	$14,201 – $54,200	$19,901 – $81,050	$9,951 – $40,525
22%	$40,526 – $86,375	$54,201 – $86,350	$81,051 – $172,750	$40,526 – $86,375
24%	$86,376 – $164,925	$86,351 – $164,900	$172,751 – $329,850	$86,376 – $164,925
32%	$164,926 – $209,425	$164,901 – $209,400	$329,851 – $418,850	$164,926 – $209,425
35%	$209,426 – $523,600	$209,401 – $523,600	$418,851 – $628,300	$209,426 – $314,150
37%	Above $523,600	Above $523,600	Above $628,300	Above $314,150

For instance, you and your spouse file jointly and make $25,000 a year. You will pay only 10% in taxes on the first $19,990 of your income and 12% for the remaining $5,100.

Taxable Income	Taxable Percentage	Tax
$19,900.00	10%	$1,990.00
$5,100.00	12%	$612.00

In this system, even the biggest earners pay the lowest rate on a part of their income. This makes taxation complex, but it has its perks. You don’t need to worry about paying a higher percentage when you get a raise.

While federal tax is based on income, the government allows you to make tax deductions on your taxable income. This means you are not required to pay tax on your total annual earnings. By law, you are entitled to a standard deduction based on your filing status. Just take note that not all personal expenses are eligible for deductions. The IRS specifies which costs you can deduct from your income.

The standard deduction is adjusted every year to keep up with inflation. For example, in 2021, filers who are single have a standard deduction of $12,550, while those who are married filing jointly (below 65 years old) have a standard deduction of $25,100. But for tax year 2020, single filers had a standard deduction of $12,400, while those married filing jointly had a standard deduction of $24,800.

Remember, maximizing deductions help lower your tax bill. If you take advantage of enough deductions, you can even reduce your tax rate for the year. For example, in 2021, let’s say you’re single and earned $47,000 for the year. When you estimated your deductions, it amounted to $7,000, which lowers your taxable income to $40,000. Based on the table above, from a tax rate of 22% at $47,000, your tax rate is reduced to 12% at $40,000.

What does this mean? If your taxable income stayed at $47,000, your tax bill would be a steep $10,340. However, because you maximized your deductions, your taxable income is reduced to $40,000. This lowered your tax bill to $4,800. Thus, you’ll save a total of $5,540 on taxes.

Interest Rates in Loans and Credit Cards

To build our lives, we make use of consumer credit for major purchases. Since a house and a car are very expensive propositions, you likely need a mortgage and auto loan to afford them. Most people also use credit cards to afford important expenses now and then pay for them later on.

When it comes to consumer credit, be mindful of the interest rate. This is the fee lending institutions charge to keep your loans serviceable. For mortgages, car loans, and credits cards, the interest is based on the annual percentage rate (APR), which is a portion or your loan amount. The interest rate determines the interest charges you must pay over the duration of your loan. Moreover, borrowing a larger loan amount will result in more expensive interest costs.

Mortgage Rates

Here’s an example comparing mortgage rates. Suppose you want to buy a $300,000 house and saved $60,000 for down payment. This leaves your total loan amount (principal) to $240,000. You’re looking to get a 30-year fixed-rate mortgage. While searching, you’re offered 4.5% and 3.8% APR. How much monthly payment and total interest will you pay for each option?

For this example, we’ll use our mortgage calculator to find the total interest costs.   

30-year Fixed-rate Mortgage
Home price: $300,000
Down payment: $60,000
Loan amount: $240,000

Interest Rate	4.5% APR	3.8% APR
Monthly Principal & Interest Payment	$1,216.04	$1,118.30
Total Interest Costs	$197,776.11	$162,587.15

*This calculation did not include escrow costs.

Based on the results, it’s a no-brainer you should get a lower interest rate. But how much can you save? If you get the 4.5% offer, your monthly payment will be $1,216.04 and your total interest charges would be $197,776.11 over the life of the loan. But with the 3.8% offer, your monthly payment will be $1,118.30, which is $97.74 cheaper than the previous offer.

Savings are more evident when we compare interest costs. With 3.8% APR, your total interest charges amount to $162,587.15. This saves you $35,188.96 on interest costs. Thus, you literally save thousands of dollars over the life of the loan just by securing a lower rate.

Credit Card Interest Rates

Next, let’s talk about credit cards. If you have a credit card balance from month to month, you should pay it ASAP. Unlike mortgages and car loans with fixed terms, credit card debt is harder to pay down. Left unpaid too long, this can spiral into toxic debt because of compound interest.

When it comes to paying debt, compound interest is not your friend. If you don’t pay your balance for the month, you end up paying interest on interest that it accrues. This interest is calculated continuously and added to your balance, which you also pay interest on. In other words, it keeps compounding. For instance, if you owe $1,000 and your interest is compounded each month at 10%, after the first month, you’ll owe $1,100. Right after the second month, you’ll owe $,1210, and so on. If you have late payments, you might also deal with expensive late fees. So be sure to pay off your balance as soon as you can.

Furthermore, credit cards are a form of unsecured debt, which means it does not use any collateral such as a house to guarantee the loan. Thus, credit cards typically impose higher interest rates than secured debt. As of May 5, 2021, CreditCards.com state that the average APR of a brand-new credit card is 16.15%. And depending on your credit score, rates can range from 13% to as high as 35%. Thus, avoid using credit cards for large expenses, unless you really need to for emergencies. Even then, make sure to pay it as soon as you can.

Important Tip!

To steer clear of compounding debt, be sure to pay your credit card balance in full every month. Diligently do this on or before the due date. The idea is to only purchase what you can afford, and to make sure you pay it in full each month. By settling your total credit card balance before interest is charged, you can avoid compounding debt. This method is called playing the float. You can only apply this strategy if you do not have any outstanding credit card balance.

Money Matters

Percentages play a crucial role in finance. Big picture percentages play a pivotal part in the fate of your personal finances. Inflation rates, for instance, show how fast your money loses value.

The financial system is built upon interest. Percentages measure the rates these fees are paid. Lenders and financial institutions base interest on specific rates. Investors receive interest on their savings accounts and investments. In exchange, companies and banks use these funds for revenue-generating enterprises. Banks, in turn, make money from the interest they earn from loans and credit.

On a smaller level, understanding percentages is essential to securing your financial future. In general, you’d want a higher rate for your savings and investments. In turn, you must find the lowest rates you can when you borrow money. Looking at percentages is but one of many factors to consider in personal finance. To know more, check out our guides on our debt management and compound savings calculators.