 Mean, Median, Mode & Range Calculator
Mean, Median, Mode & Range Calculator

Calculate Average and Range
Math Definition
- Mean
- The average of all the data in a set.
- Median
- The value in a set which is most close to the middle of a range.
- Mode
- The value which occures most frequently in a data set.
- Range
- The difference between the largest and smallest data in a data set.
Example Calculation
Calculate the mean, median, mode and range for 3, 19, 9, 7, 27, 4, 8, 15, 3, 11.
How to Find the Mean (or Average Value)
To figure the mean, add up the numbers, 3+3+4+7+8+9+11+15+19+27=106 then divide it by the number of data points 106/10=10.6.
How to Find the Median
In ascending order the numbers are 3, 3, 4, 7, 8, 9, 11, 15, 19, 27. There are 10 total numbers, so the 5th and 6th numbers are used to figure the median. (8+9)/2 = 8.5
If there were 9 numbers in the series rather than 10 you would take the 5th number and would not need to average the 2 middle numbers. The 2 middle numbers only need to be averaged when the data set has an even number of data points in it.
How to Find the Mode
The only number which appears multiple times is 3, so it is the mode.
How to Find the Range
To figure the range subtract the smallest number from the largest number 27-3=24.
Mean, Median and Mode: Data Trends, Detecting Anomalies, and Uses in Sports
- Guide Authored by Corin B. Arenas, published on October 17, 2019
In school, we ask the average score for a test to know if we have a good grade. When it comes to buying expensive products, we often ask the average price to look for the best deals.
These are just a few examples of how averages are used in real life.
In this section, you’ll learn about the different types of averages and how they’re calculated and applied in various fields, especially in sports.
What Does the Term ‘Average’ Mean?

When people describe the ‘average’ of a group of numbers, they often refer to the arithmetic mean. This is one out of 3 different types of average, which include median and mode.
| Types of Average | Description |
|---|---|
| Mean | The average of numbers in a group. |
| Median | The middle number in a set of numbers. |
| Mode | The number that appears most often in a set of numbers. |
In conversational terms, most people just say ‘average’ when they’re really referring to the mean. Arithmetic mean and average are synonymous words which are used interchangeably, according to Dictionary.com.
It’s calculated by adding the numbers in a set and dividing it by the total number in the set—which is what most people do when they’re finding the average. See the example below.
Mean
Set: 8, 12, 9, 7, 13, 10
Mean = (8 + 12 + 9 + 7 + 13 + 10) / 6
= 59 / 6
= 9.83
The average or arithmetic mean in this example is 9.83.
Median
The median, on the other hand, is another type of average that represents the middle number in an ordered sequence of numbers. This works by ordering a sequence of numbers (in ascending order) then determining the number which occurs at the middle of the set. See the example below.
Average Median
Set: 22, 26, 29, 33, 39, 40, 42, 47, 53
In this example, 39 is the median or middle value in the set.
Mode
The mode is basically the most frequent value that repeats itself in a set of values. For instance, if your set has 21, 9, 14, 3, 11, 33, 5, 9, 16, 21, 5, 9, what is the mode?
The answer is 9 because this value is repeated 3 times.
In statistics, mean, median, and mode are all terms used to measure central tendency in a sample data. This is illustrated by the normal distribution graph below.
The normal distribution graph is used to visualize standard deviation in data analysis. Distribution of statistical data shows how frequent the values in a data set occurs.
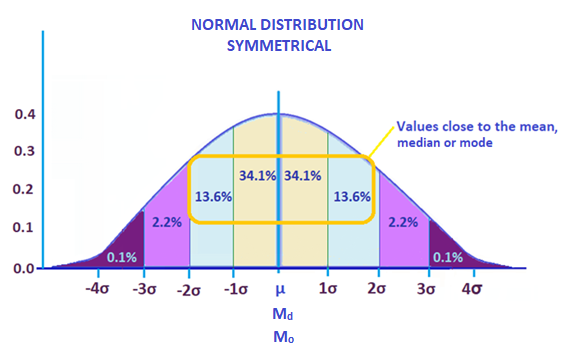
In the graph above, the percentages represent the amount of values that fall within each section. The highlighted percentages basically show how much of the data falls close to middle of the graph.
What is the Relationship Between Mean, Median and Mode?

At first glance, it would seem like no connection exists between mean, median, and mode. But there is an empirical relationship that exists in measuring the center of a data set.
Mathematicians have observed that there is usually a difference between the median and the mode, and it is 3 times the difference between the mean and the median.
The empirical relationship is expressed in the formula below:
Mean – Mode = 3(Mean – Median)
Let’s take the example of population data based on 50 states. For instance, the mean of a population is 7 million, with a median of 4.8 million and mode of 1.5 million.
- Mean = 7 million
- Median = 4.8 million
- Mode = 1.5 million
Mean – Mode = 3(Mean – Median)
7 million – 1.5 million = 3(7 million – 4.8 million)
5.5 million = 3(2.2)
5.5 million = 6.6 million
Take note: Mathematics professor Courtney Taylor, Ph.D. stated that it is not an exact relationship. When you do calculations, the numbers are not always precise. But the corresponding numbers will be relatively close.
Asymmetrical or Skewed Data

According to Microeconomicsnotes.com, when the values of the mean, median and mode are not equal, the distribution is asymmetrical or skewed. The degree of skewness represents the extent to which a data set varies from the normal distribution.
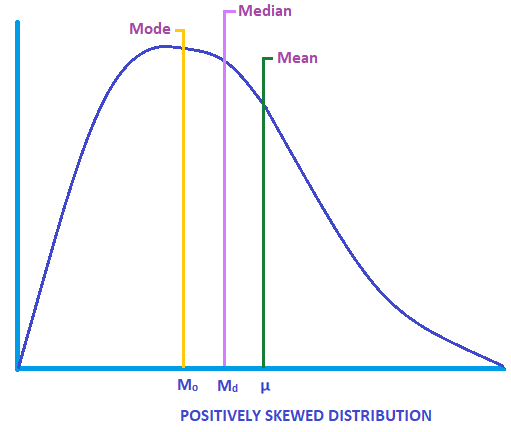
When the mean is greater than the median, and the median is greater than the mode (Mean > Median > Mode), it is a positively skewed distribution. It’s described as ‘skewed to the right’ because the long tail end of the curve is towards the right.
In the sample graph below, the median and mode are located to the left of the mean.
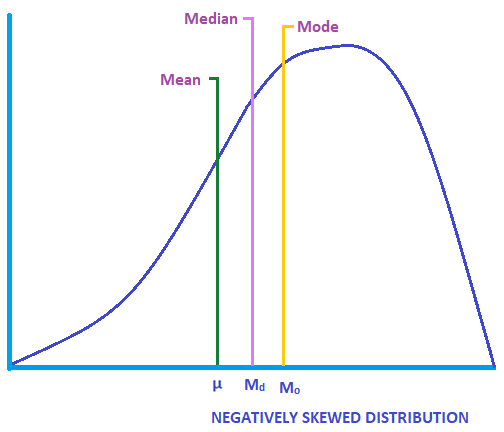
On the other hand, in a negatively skewed distribution, the mean is less than the median, and the median is less than the mode (Mean < Median < Mode). The longtail end is located towards the left side of the graph.
The graph below shows the median and mode located to the right side of the mean.
Varying Mean from Median: Resistant Numerical Summaries

In a data set, when the mean is high, a reader might assume the median will also be high. However, this does not always follow.
The difference between mean and median becomes apparent when a data set has an outlying disparate value. This situation calls attention to the concept of resistant numerical summaries. A resistant statistic is a numerical summary wherein extreme numbers do not have a substantial impact on its value.
Let’s show this by demonstrating how Bill Gates’ presence impacts mean and median wealth when he walks into a room.
For instance, 10 people are having dinner at a restaurant. Let’s call it set A. The table below shows their income from lowest to highest.
| Name | Annual Income |
|---|---|
| Raffy | $33,000 |
| Jessie | $38,000 |
| Corin | $39,000 |
| Paul | $42,000 |
| Kat | $46,000 |
| Luigi | $49,000 |
| Carl | $52,000 |
| Susan | $60,000 |
| Miguel | $68,000 |
| John | $79,000 |
The total income of the people in the restaurant is $506,000, with a mean income of $50,600.
Since there are 10 people in the set, to get the median, we have to add the 5th and 6th values (Kat and Luigi’s annual income) and divide it by 2.
Median = (46,000 + 49,000) / 2= 95,000/2
= 47,500
The median income of the group is $47,500.
The range is the difference between the lowest income (Raffy) and the highest income (John), which is $46,000.
Set A Annual Income
| Total Income | $506,000 |
| Mean | $506,000 |
| Median | $47,500 |
| Range | $46,000 |
Now, if John leaves the restaurant and Bill Gates walks in, how will it affect the group’s annual income stats? Let’s call this next group set B.
According to Forbes, Bill Gates made $90 billion from 2017 to 2018.
| Name | Annual Income |
|---|---|
| Raffy | $33,000 |
| Jessie | $38,000 |
| Corin | $39,000 |
| Paul | $42,000 |
| Kat | $46,000 |
| Luigi | $49,000 |
| Carl | $52,000 |
| Susan | $60,000 |
| Miguel | $68,000 |
| Bill Gates | $90,000,000,000 |
Set B Annual Income
| Total Income | $90,000,427,000 |
| Mean | $9,000,042,700 |
| Median | $47,500 |
| Range | $89,999,967,000 |
With Bill Gates, the total income is now $90 billion plus the lower income of the people in the restaurant. The mean income and the range of the group is now too high.
However, the median remains the same at around $47,500.
The median shows it’s a better indication of people’s actual financial status. Likewise, we can say Bill Gates is an outlier with an annual income that hits billions.
This example shows that the mean and range are not resistant to extreme values. While the median, as a numerical summary, generally exhibits resistance.
What does this tell us? The presence of extreme values or outliers indicate that a distribution is skewed. Extreme values typically pull the mean toward the direction of the tail.
The Significance of Identifying Skewness

Observing skewness in a graph gives analysts a clearer idea of a data set’s trend. For instance, if you collected data from 500 students that took the Scholastic Assessment Test, you’d want to know the score trend.
If you plot the data in a graph, you’d know it’s positively skewed if there are few high scores and most of the values are clustered towards the lower side of the scale. If the scores tend toward the higher side of the scale, with few low scores, the distribution is negatively skewed.
In finance, investors take note of skewness when they analyze return distribution. This is important because it allows them to see the extreme ranges of the data instead of just focusing on the average values.
A distribution shows skewness (degree of asymmetry) or kurtosis when the returns fall outside the normal distribution. Kurtosis measures the outliers in either tail of a skewed graph. It calculates the degree to which a graph is peaked compared to a normal distribution.
How does it help investors? Observing skewness or kurtosis helps analysts predict risks that that result when a model following normal distribution is compared to a data set with a tendency for higher standard deviation. The risk is determined by calculating how far the numbers are from the normal distribution.
How to Identify Data Anomalies
In statistics, outliers or anomalies are unusual observations that do not belong to a certain population.
When placed in a graph, these are points that fall far away from the data set’s values. Researchers commonly find outliers based on large, well-structured data.
How different should a value be to be considered an outlier? To determine this, you can use the interquartile range (IQR).
IQR is described as a 5 number summary, which contains:
- The minimum value of a data set
- The first quartile (Q1) – Which is a quarter of the way through the sequence of a data set
- The median
- The third quartile (Q3) Which is three quarters of the way through the sequence of all data
- The maximum value of the data set
The interquartile range (IQR) is also similar to range but is considered a less sensitive to extreme values (resistant statistic). To find it, you must take the first quartile and subtract the third quartile. This shows how data is spread around the median.
IQR = Q3 – Q1
Detecting Outliers Using IQR
Practically all sets of data can be described by the 5 number summary. Here’s how you can use IQR to find outliers:
- Compute the interquartile range for the data set
- Multiply the IQR by 1.5
- Add IQR x 1.5 to the third quartile. The rule: Any value greater that this is an outlier.
- Subtract IQR x 1.5 from the first quartile. The rule: Any value less than this is an outlier.
Here’s an example. Suppose you’re finding the outlier for the data set below:
1, 5, 6, 6, 9, 10, 10, 11, 12, 13, 18
5 number summary:
- Minimum value = 1
- Q1 = 6
- Median = 10
- Q3 = 12
- Maximum value = 18
IQR = Q3 – Q1
= 12 – 6
IQR = 6
IQR x 1.5 = ?
6 x 1.5 = 9
9 + Q3 = ?
9 + 12 = 21 (any value greater than 21 is an outlier)
6 – Q1 = ?
6 – 9 = -3 (any value less that -3 is an outlier)
So far, no value is less than -3 or greater than 21 in the set. Though the maximum value 18 is 5 points more than 13, it is not considered an outlier for this data set.
How Statistic Averages are Used in Sports Analytics

In sports analytics, researchers gather statistics to measure the potential and ability of professional athletes.
According to Competitive Edge Athletic Performance Center, sports performance metrics are relevant to overall athletic development. To achieve success in any sports field, individuals must reach certain levels of athleticism to compete at advanced levels.
In fact, many professional sports teams consult statisticians to help athletes track their competitive advantage. This guides them in improving their strength and conditioning routines.
Tracking performance metrics helps athletes do 4 crucial things:
- Helps them know their current level or baseline.
- Once they improve, it allows them to compete at higher sports levels.
- Allows athletes to identify individual training needs.
- Can help lower the risk of injuries.
Popular Sports Averages

Batting average (BA) is a performance statistic used in baseball, cricket and softball. It measures the number of average runs a player can score before getting out.
It’s the oldest measuring tool that gauges a batter’s success. Higher BA means the batter has greater potential to score runs without getting an out.
The BA is calculated by dividing a player’s hits by his total at-bats, for a value between .000 and 1.000.
According to the Major League Baseball website, the league-wide BA in recent years has remained around .260. For the game’s best batters, they can exceed .300.
However, some exceptional athletes have hit above .400, which is 4 hits for every 10 at-bats. MLB states no player has done this throughout a full season since Ted Williams (.406) of Boston Red Sox in 1941.
In the strike-shortened 1994 season Tony Gwynn came close to hitting 400, batting 394 with 164 hits on 419 at bats in 110 games.
Here’s a table of MLB players showing the regular season batting average leaders from 1985 to 2019 :
| Year | National League Leader | NL Team | BA | American League Leader | AL Team | BA |
|---|---|---|---|---|---|---|
| 2019 | Christian Yelich | MIL | .329 | Tim Anderson | CHW | .335 |
| 2018 | Christian Yelich | MIL | .326 | Mookie Betts | BOS | .346 |
| 2017 | Charlie Blackmon | COL | .331 | Jose Altuve | HOU | .346 |
| 2016 | DJ LeMahieu | COL | .348 | Jose Altuve | HOU | .338 |
| 2015 | Dee Gordon | MIA | .333 | Miguel Cabrera | DET | .338 |
| 2014 | Justin Morneau | COL | .319 | Jose Altuve | HOU | .341 |
| 2013 | Michael Cuddyer | COL | .331 | Miguel Cabrera | DET | .348 |
| 2012 | Buster Posey | SFG | .336 | Miguel Cabrera | DET | .330 |
| 2011 | Jose Reyes | NYM | .337 | Miguel Cabrera | DET | .344 |
| 2010 | Carlos Gonzalez | COL | .336 | Josh Hamilton | TEX | .359 |
| 2009 | Hanley Ramirez | FLA | .342 | Joe Mauer | MIN | .365 |
| 2008 | Chipper Jones | ATL | .364 | Joe Mauer | MIN | .328 |
| 2007 | Matt Holliday | COL | .340 | Magglio Ordonez | DET | .363 |
| 2006 | Freddy Sanchez | PIT | .344 | Joe Mauer | MIN | .347 |
| 2005 | Derrek Lee | CHC | .335 | Michael Young | TEX | .331 |
| 2004 | Barry Bonds | SFG | .362 | Ichiro Suzuki | SEA | .372 |
| 2003 | Albert Pujols | STL | .359 | Bill Mueller | BOS | .326 |
| 2002 | Barry Bonds | SFG | .370 | Manny Ramirez | BOS | .349 |
| 2001 | Larry Walker | COL | .350 | Ichiro Suzuki | SEA | .350 |
| 2000 | Todd Helton | COL | .372 | Nomar Garciaparra | BOS | .372 |
| 1999 | Larry Walker | COL | .379 | Nomar Garciaparra | BOS | .357 |
| 1998 | Larry Walker | COL | .363 | Bernie Williams | NYY | .339 |
| 1997 | Tony Gwynn | SDP | .372 | Frank Thomas | CHW | .347 |
| 1996 | Tony Gwynn | SDP | .353 | Alex Rodriguez | SEA | .358 |
| 1995 | Tony Gwynn | SDP | .368 | Edgar Martinez | SEA | .356 |
| 1994 | Tony Gwynn | SDP | .394 | Paul O'Neill | NYY | .359 |
| 1993 | Andres Galarraga | COL | .370 | John Olerud | TOR | .363 |
| 1992 | Gary Sheffield | SDP | .330 | Edgar Martinez | SEA | .343 |
| 1991 | Terry Pendleton | ATL | .319 | Julio Franco | TEX | .341 |
| 1990 | Willie McGee | STL | .335 | George Brett | KCR | .329 |
| 1989 | Tony Gwynn | SDP | .336 | Kirby Puckett | MIN | .339 |
| 1988 | Tony Gwynn | SDP | .313 | Wade Boggs | BOS | .366 |
| 1987 | Tony Gwynn | SDP | .370 | Wade Boggs | BOS | .363 |
| 1986 | Tim Raines | MON | .334 | Wade Boggs | BOS | .357 |
| 1985 | Willie McGee | STL | .353 | Wade Boggs | BOS | .368 |
In basketball, field goal percentage (FG) is used to measure how effectively a team scores a ball during a game.
FG considers all shots taken by a player. However, it doesn’t include free throws that are measured independently as free throw percentage.
The formula for FG is the number of successful shots divided by the total number of shot attempts.
An FG of .500 or 50% and up is usually considered a good percentage. According to Basketball Reference, the active player with the highest percentage is currently DeAndre Jordan, with 66.96%.
Notable basketball players like Michael Jordan have an FG of 49.69% with a ranking of 151, while Lebron James ranks at 111 with 50.42%. Hall of famers like Kareem Abdul-Jabbar ranks at 14 with 55.95%, while Magic Johnson ranks at 64 with 51.97%.
Basketball Reference identified the 4 factors that help teams win games:
- Shooting (40%)
- Turnovers (25%)
- Rebounding (20%)
- Free Throws (15%)
Out of the 4, shooting is the most important factor, followed by turnovers, rebounding and free throws. However, others would argue that apart an effective field goal percentage, a game is won with a solid defense strategy.
Below is a table of NBA players with the highest field goal percentage.
Active players are in bold.
* Indicates a member of the Hall of Fame
| Rank | Name | FG% |
|---|---|---|
| 1. | DeAndre Jordan | .6696 |
| 2. | Artis Gilmore* | .5990 |
| 3. | Tyson Chandler | .5960 |
| 4. | Dwight Howard | .5828 |
| 5. | Shaquille O’Neal* | .5823 |
| 6. | Mark West | .5803 |
| 7. | Steve Johnson | .5722 |
| 8. | Darryl Dawkins | .5720 |
| 9. | James Donaldson | .5706 |
| 10. | JaVale McGee | .5697 |
| Amir Johnson | .5697 | |
| 12. | Bo Outlaw | .5673 |
| 13. | Jeff Ruland | .5637 |
| 14. | Kareem Abdul-Jabbar* | .5595 |
| 15. | Jonas Valančiūnas | .5583 |
| 16. | Kevin McHale* | .5538 |
| 17. | Marcin Gortat | .5514 |
| 18. | Bobby Jones* | .5504 |
| 19. | Buck Williams | .5492 |
| 20. | Nenê Hilário | .5478 |
Many field goal percentage leaders are big men who tend to dunk & shoot other high percentage inside shots. In recent years the 3-point shot has become more widely used. A mark of a great all around shooting performance is 50-40-90, where a player has a 50% FG, 40% from 3-point range, and 90% from the free throw line.
The Bottom Line
There are three types of averages, and these are the mean, median and mode. Out of the three, the most commonly used is the arithmetic mean. It’s determined by adding all the values in a set and dividing it by the total number of factors.
Calculating mean, median and mode allows researchers to observe normal distribution or skewness in a graph. In finance, investors use this to measure the risk of return distribution. To detect statistical outliers, analysts use the interquartile range.
Computing averages is particularly relevant in sports analytics. It’s used to set benchmarks and improve athletic performance. Metrics help athletes streamline strength and conditioning routines, as well as avoid injuries.
About the Author
Corin is an ardent researcher and writer of financial topics—studying economic trends, how they affect populations, as well as how to help consumers make wiser financial decisions. Her other feature articles can be read on Inquirer.net and Manileno.com. She holds a Master’s degree in Creative Writing from the University of the Philippines, one of the top academic institutions in the world, and a Bachelor’s in Communication Arts from Miriam College.
When in Doubt, Autosum ;)


