 Fraction Calculator
Fraction Calculator

Usage Instructions
- Enter your fractions in the above calculator.
- Select the mathematical operation you would like to perform (add, subtract, multiply, divide) using the gray dropdown select box between the two fractions.
- Results will update automatically whenever you change any of the values in the calculator.
- A checkbox below the calculator allows you to select between reducing the fraction to the lowest common denominator equivalent (if checked) or not reducing it (if unchecked).

How to Manually Calculate Fractions
How to Add Fractions
- Find the lowest common denominator by multiplying each denominator by the other.
- Multiply each numerator by the same numbers the denominators were multiplied by.
- Add the numerators together.
- Reduce result to most simplified number.
How to Subtract Fractions
- Find the lowest common denominator by multiplying each denominator by the other.
- Multiply each numerator by the same numbers the denominators were multiplied by.
- Add the second numerator from the first.
- Reduce result to most simplified number.
How to Multiply Fractions
- Multiply the numbers across the top together.
- Multiply the numbers across the bottom together.
- Reduce result to most simplified number.
How to Divide Fractions
- Turn the second fraction upside down to create the reciprocal number.
- Multiply the fractions together (just like in the multiplication section above).
- Reduce result to most simplified number.
Fractions: History, Relevance, and Popular Uses
- Guide Authored by Corin B. Arenas, published on October 22, 2019
We practically deal with fractions every day. Think about it. Whether you get quarters for a change, buy outfits at 75% off, or cook with half a cup of butter, you’re using fractions.
In this section, we’ll talk about the origin of fractions, its importance in how information is delivered, and the golden ratio.
What are Fractions?
Fractions represent parts of a whole number, or any number of equal parts. It functions to describe how the parts relate with the whole number.
To illustrate, think of a whole number like a cake. If you slice the cake into 4 equal parts, one slice is a fraction of that cake. In this case, it’s 1/4 of the entire cake.
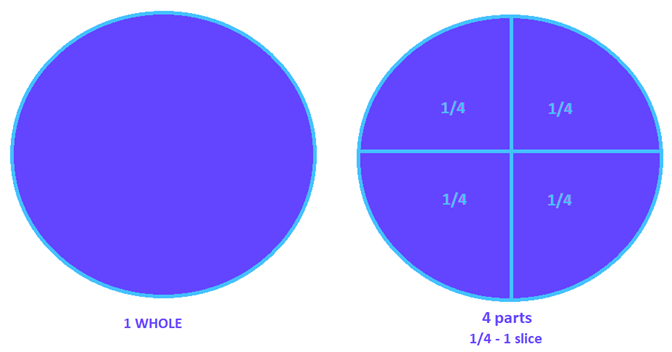
- 1 represents one slice or part of the whole number, which is called the numerator.
- 4 represents how many total parts are in a whole number, which is called the denominator.

A Brief History of Fractions
Word Origin: The term fraction comes from the Latin word fractio which means ‘breaking.’ In early English, it suggests a ‘broken off piece or fragment.’ The English word ‘fracture’ also has the same word origin.
The concept of fractions has been around for more than 4,000 years. But different civilizations have their own way of standardizing fractions for universal use.
Egyptians

According to Math Through the Ages: A Gentle History for Teachers and Others, the Egyptians were one of the first to devise a form of fraction as early as 1800 B.C. Their concept was mainly limited to parts, otherwise known as unit fractions. Unit fractions use 1 as its numerator.
Egyptian mathematicians created a system with a base 10 idea, which is similar to number systems we use today. Numeral hieroglyphs represented their numbers, which means symbols corresponded to a particular value.
Since the numerator is always 1, they only had to indicate the denominator. Egyptians marked the denominator with an oval or dot on top of the value. Here are a few examples from Math Through the Ages:

Parts were expressed as sums of unit fractions. However, the system did not allow unit fractions to be repeated in this sequence, making it difficult to do calculations. To resolve the problem, Egyptians created extensive table listings that supplied the double values of various parts.
Babylonians

Another civilization that created an elaborate system for fractions were the Babylonians, according to mathematics instructor and author Liz Pumfrey.
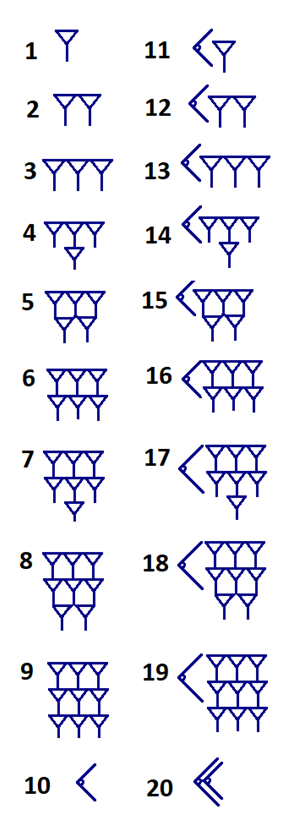
Babylonians organized fractions in groups of 60 (base 60). Today, we usually organize numbers in groups of 10. But for calculations like angles and minutes for time, we also use base 60. The system grouped fractions in 10s and used two symbols, one for unit and another for 10.
Below are the symbols representing the Babylonian numeral system from numbers 1-20:
However, they didn’t have a symbol for zero (which they later added around 311 B.C.) or a mark that functions as a decimal point to indicate fractions of a whole number. This made it confusing to interpret numbers.
For instance, the numbers below are read as 12 and 15.
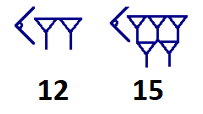
According to Pumfrey, the symbols can also be read as different values:
| x60 | Units | Sixtieths | Number |
|---|---|---|---|
| 12 | 15 | ||
| 12 | 15 | 720 + 15 |
- 12 and 15 as separate numbers
- 12/15
- 12 15/60
- 720 + 15
As you can see, the absence of a fraction indicator makes it hard to separate whole numbers from fractions. They likely relied on context to make sense of the numerical values.
Both Egyptian and Babylonian systems were passed on later to people in Greece, and then to the Mediterranean civilization.
Greeks

In Greece, the practice of using fractional values as sums of unit fractions was fairly common until the Middle Ages. For example, Liber Abbaci by Italian mathematician Fibonacci is a notable 13th century text. It made extensive use of fractions, describing different ways of converting other fractions into sums of unit fraction.
To understand it better, below is a table of Greek numeral symbols. Note that they are the same as the letters in the Greek alphabet:
| Value | Units | Tens | Hundreds |
|---|---|---|---|
| 1 | α | ι | ρ |
| 2 | β | κ | σ |
| 3 | γ | λ | τ |
| 4 | δ | µ | υ |
| 5 | ε | ν | φ |
| 6 | ϝ | ξ | χ |
| 7 | ζ | ο | ψ |
| 8 | η | π | ω |
| 9 | θ | ϙ | ϡ |
Greek notation of fractions requires readers to understand context for proper interpretation. To set a fraction apart, they place a diacritical mark (‘) after the denominator of a fraction.
For instance, the number β (2) becomes ½ when written with a diacritical mark, β’.
Likewise, µβ (42) becomes 1/42 when written in µβ’.
However, this is where it becomes confusing: µβ’ could also mean 40 ½. That’s why understanding context is crucial in interpreting Greek fractions.
Romans
For Romans, fractions were only expressed using words, which made it more difficult to do any calculations.
Their system was based on a unit of weight called ‘as.’ Following this approach, 1 ‘as’ was equal to 12 uncia (Rome’s basic unit of measurement, the basis for the modern ounce). Thus, the fractions have denominators with values divisible by 12.
The table below shows Roman fractions with their corresponding terms:
| Fraction | Roman Term |
|---|---|
| 11/12 | deunx for de uncia, 1/12 taken away |
| 10/12 | dextans for de sextans, 1/6 taken away |
| 9/12 | dodrans for de quadrans, 1/4 taken away |
| 8/12 | bes – bi as for duae partes, 2/3 |
| 7/12 | septunx for septem unciae |
| 6/12 | semis |
| 5/12 | quincunx for quinque unciae |
| 4/12 | triens |
| 3/12 | quadrans |
| 2/12 | sextans |
| 1/12 | uncia |
| 1/24 | semuncia |
| 1/48 | sicilicus |
| 1/72 | scriptulum |
| 1/144 | scripulum |
| 1/288 | scrupulum |
Chinese

The Chinese wrote the Nine Chapters on the Mathematical Art, which dates back to around 100 B.C. It includes text on fractions that are similar to the ones we use today.
According to Math Through the Ages, it contained most of the usual rules for calculating with fractions, such as how to add, divide and multiply fractions, as well as reduce a fraction to its lowest terms.

However, their system avoided using improper fractions. For instance, instead of the improper fraction 9/4, they would use its equivalent mixed fraction, 2 1/4.
Unlike Western Mathematics, the Chinese focused on practical applications rather than theoretical reasoning and geometry.

Indians

The Indians developed a way of writing fractions that’s much closer to what we use today.
Before 1000 B.C., Hindu mantras during the early Vedic period would invoke powers of ten from a hundred, even up to a trillion, according to resource site, The Story of Mathematics. This is evidence that early Indian civilization used complex mathematical operations, including fractions, squares, cubes and roots.
Around 500 B.C., they came up with a writing system called brahmi that consisted of 9 numerical symbols and a zero. Mathematics teacher and author Liz Pumfrey notes that these numbers largely influenced the modern numbers we use today. See the image below.
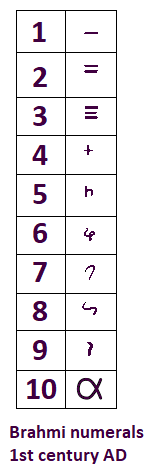
The Indian system wrote fractions by placing one value on top of another, just like how the numerator is written above the denominator today. However, they did not place a line in between it. For instance, the fraction 4/5 would look like this:
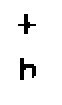
Later on, the system was used by the Arabs while trading with the Indians. It was the Arabs who drew a line to distinguish the top number from the lower number in the fraction. This eventually led to the way we write fractions in the modern age.
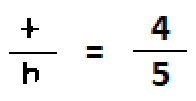
How Fractions Improve the Way Information is Conveyed

According to Doctor Peterson of MathForum.org: “fractions were invented to provide a way to work with quantities smaller than one.”
If people only used whole numbers, the only way to refer to smaller quantities is to use smaller units. This is what the Romans did—they used whole numbers in measuring feet and used inches when they needed to account for smaller units.
For instance, instead of 1/12 of a foot, they would refer to the length as 1 inch, and 1/4 of a foot would be 3 inches. But what if you’re referring to 2 feet and a half? How about 1 and 3/4 feet?
If you are basing a standard length according to feet, it’s confusing to keep referring to feet and inches at the same time. Basically, fractions make it possible to provide measurements without necessarily creating new units. It would make better sense to account for the measurements in a consistent fashion.
The U.S. tends to use fractions more (English measurement) as they use cups rather than scales for measuring when cooking and baking.
Americans have yet to adopt to the metric system, which is a decimal-based system that uses units that are related to factors of 10. The metric system usually uses grams and liters in place of the American measurement for ounces, cups, pints and so on.
The table below provides volume conversion from English measurement to its metric equivalent:
US to Metric Volume Conversions
| US Customary Quantity (English) | Metric Equivalent |
|---|---|
| 1 teaspoon | 5 mL |
| 1 tablespoon | 15 mL |
| 2 tablespoons | 30 mL |
| 1/4 cup or 2 fluid ounces | 60 mL |
| 1/3 cup | 80 mL |
| 1/2 cup or 4 fluid ounces | 125 mL |
| 2/3 cup | 160 mL |
| 3/4 cup or 6 fluid ounces | 180 mL |
| 1 cup or 8 fluid ounces or 1/2 pint | 250 mL |
| 1 ½ cup or 12 fluid ounces | 375 mL |
| 2 cups or 1 pint or 16 fluid ounces | 500 mL |
| 3 cups or 1 ½ pints | 700 mL |
| 4 cups or 2 pints or 1 quart | 950 mL |
| 4 quarts or 1 gallon | 3.8 L |
| 1 ounce | 28 grams |
| 1/4 lb. (4 ounces) | 112 grams |
| 1/2 lb. (8 ounces) | 225 grams |
| 3/4 lb. (12 ounces) | 337 grams |
| 1 lb. (16 ounces) | 450 grams |
Moreover, keeping the measurements in one unit allows us to add, subtract, multiply and divide fractions easily. This eliminates the problem of conversion, which is not possible if a measurement is between two different units.
For an easier way to calculate fractions, just use the calculator on top of this page.
While decimals provide an alternative way of indicating fractions (and an easier way to calculate fractions using a calculator), it is imperative to understand traditional fractions and how their values affect a whole number.
According to Thoughtco.com, students who do not master fractions in their early years have a tendency to get confused and experience math anxiety. They also mentioned half of American eight graders cannot arrange fractions in order of value.
Learning fractions intuitively helps children develop wider understanding of theoretical math concepts, allowing them to use it in real life. That’s far better than memorizing tables with units or symbols.
The Golden Ratio and the Fibonacci Sequence

In mathematics, a ratio is essentially a comparison of two numbers which depend on the kind of numbers being compared.
You might encounter an example written like this: 1:3, or 1 of 3. For instance, a bottle of orange juice concentrate is made of 1 part orange juice and 3 parts water. This can also be written as a fraction, 1/3.
Ratios are related to fractions because they compare different values which might represent a whole. In this example, the whole part is the bottle of orange juice.
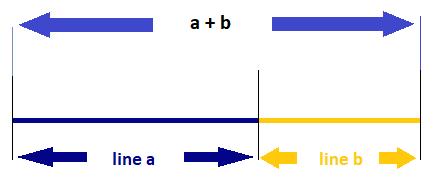
The Golden Ratio is a special number represented by the Greek symbol phi (φ) with an approximate value of 1.618.
It’s derived by dividing a line in 2 parts so that the long section (a) divided by the short section (b) is equal to the entire length divided by the long section.
To give you a better idea, here’s an illustration with the standard equation:
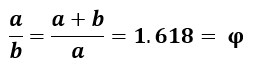
Historically, the ratio is said to be observed in ancient structures like the Parthenon and the Pyramids of Egypt. In the Great Pyramid of Giza, the ratio of the base to the height is approximately 1.5717, which is close to the Golden ratio. It’s also found in recurring patterns in nature such as flower petals, seashells, tree branches and spiral galaxies.
On the other hand, the Fibonacci sequence is another famous formula in math. The sequence is derived from the sum of two numbers that precede it. Many sources say Leonardo Fibonacci (Leonardo of Pisa) popularized it in his book Liber Abacci.
But according to Live Science, mathematician Keith Devlin, author of Finding Fibonacci: The Quest to Rediscover the Forgotten Mathematical Genius Who Changed the World, states that Leonardo Fibonacci did not actually ‘discover’ the sequence.
Ancient Sanskrit writings that used the Hindu-Arabic numeral system were the first to discuss it centuries before Leonardo Fibonacci.
The Fibonacci sequence goes like this:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, and so on…
When mathematicians create squares based on this sequence, they can draw a spiral.
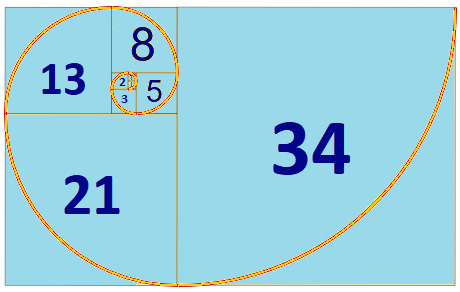
How is the Golden Ratio related to the Fibonacci Sequence?
Researchers observed that when you take any two successive Fibonacci numbers, their ratio is very close to the golden ratio. So φ is approximately 1.618. To give you an idea, see the table below.
| A | B | B / A |
|---|---|---|
| 2 | 3 | 1.5 |
| 3 | 5 | 1.666666666… |
| 5 | 8 | 1.6 |
| 8 | 13 | 1.625 |
The Bottom Line
The concept of fractions were developed by different ancient civilizations. One of the earliest to devise a fractional system with extensive tables were the Egyptians. Other ancient societies like Babylonians, Greeks, Romans and Chinese also contributed to its improvement. But modern numerals and the way we write fractions were mostly influenced by Indians who introduced the Hindu-Arabic numerical system.
Using fractions help us convey information on measurements easily. It keeps people from using different units of measurement, making it easier to calculate them.
Finally, fractions are related to the famous Golden Ration and Fibonacci sequence, which has largely influenced the way we design all kinds of structures.
About the Author
Corin is an ardent researcher and writer of financial topics—studying economic trends, how they affect populations, as well as how to help consumers make wiser financial decisions. Her other feature articles can be read on Inquirer.net and Manileno.com. She holds a Master’s degree in Creative Writing from the University of the Philippines, one of the top academic institutions in the world, and a Bachelor’s in Communication Arts from Miriam College.
Funny Math Cartoons


